Global Illumination via Photon Mapping

During our computer graphics class at MIT (6.837) in Fall 2021, a class partner and I embarked on an exciting project to solve the problem of global illumination. Our aim was to move beyond the simplistic approach of ambient lighting in the Phong shader model and develop a more realistic model that simulates light bouncing around surfaces and reflecting onto other surfaces, creating global illumination. Working together, we chose to implement photon mapping, optimized using a k-d tree data structure. Additionally, we incorporated refraction to power caustics, contributing to a more authentic rendering of the scene.

Refraction

Our refraction implementation was based on a University of Washington lecture by Daniel Leventhal. We extended our standard ray tracer, which already supported recursive ray bounces for reflection. For refraction, we calculated the angle using Snell’s law, factoring in the index of refraction of the intersected object, and assumed solid glass surfaces for simplicity. We also accounted for total internal reflection using Snell’s law, which resulted in a reflected ray instead of a refracted one for certain ray angles.

Photon Mapping

Our photon mapping work was based on the paper “A Practical Guide to Global Illumination using Photon Maps” by Niels Jorgen Christensen and Henrik Wann Jensen, presented at Siggraph 2000. We created the photon map by casting rays randomly from a point light, with each ray representing a photon carrying a portion of the light’s energy. Photons could undergo diffuse reflection, specular reflection, absorption, or refraction upon intersection with an object. To implement caustics, we created a secondary photon map that cast more photons but only stored interactions with refractive materials.

We determined each photon’s action on intersection using a technique called “Russian Roulette,” which allowed us to manage the space and time complexity more efficiently. A random number was generated in order to decide the fate of each individual photon for each interaction with an object, based on the contacted material’s properties, specifically diffuse and specular color, as well as assigned values for refraction and reflection, which were used to calculate probabilities of diffuse reflection, specular reflection, absorption, and refraction.

For gathering photons, we employed a radiance estimate function that collected all photons within a radius r of the point where the eye rays intersected an object. The power of each photon was scaled based on a cone filter and its contribution to the light at that point, allowing us to approximate the global illumination contribution at that point.

k-d Tree Data Structure

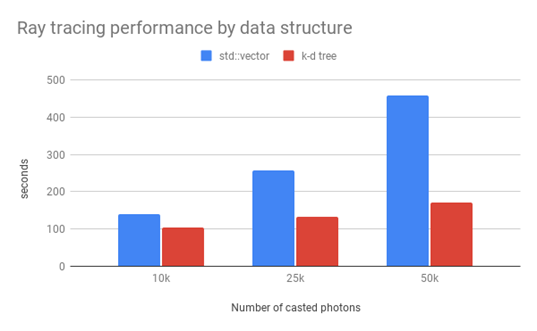
Our k-d tree data structure, also based on “A Practical Guide to Global Illumination using Photon Maps” and the k-d tree implementation published on Rosetta Code, supported the building and balancing of the tree and the GetNeighbors() operation to retrieve nearby photons quickly during the ray tracing process, making rendering much faster than it would be otherwise.

Results and Future Work

We successfully solved the problem of global illumination using photon mapping, supported by refraction, caustics, and a k-d tree to accelerate the photon gathering step during ray tracing. However, there are potential future improvements, such as extending the refraction implementation to include different materials and using the Fresnel equation, implementing more complex filtering techniques or adding photon mapping for volumetric objects, and expanding the capabilities of the k-d tree.