Mesh Simplification for Accelerated Physics Simulation

Introduction

Physics simulations are an integral part of computationally-aided design workflows, such as animation and modeling. However, these simulations can be time-consuming. To address this issue, for our final project in the MIT course MIT Computational Design and Fabrication (6.8420) in Fall 2022, my partner and I developed an approximation algorithm that produces accurate yet fast physics simulations. Our algorithm involves creating a decimated copy of the target mesh, running the intended physics simulation on this copy, and then translating simulation deformation from the decimated copy to the target mesh using weighted handles.

My Role

In this project, my primary focus was on the mesh simplification algorithms, while my partner worked on the interpolation/approximation step, which would mirror the simulation step from the low resolution model to the high resolution model. To reach this end, I referenced research on mesh and volume decimation methodology, including the Garland-Heckbert mesh decimation using quadric error metrics method and Van Gelder volume decimation method.

Method

Our method involves three main steps:

1. Decimate the target mesh: We employed two separate algorithms, the Garland-Heckbert mesh decimation and the Van Gelder volume decimation.
2. Run a physics simulation on the decimated mesh: We used a finite element method (FEM) non-linear physics simulation.
3. Mirror the simulation deformation on the decimated mesh on the target mesh: We used weighted handles, inspired by their ability to quickly deform meshes, and the KD Tree data structure.

Mesh Decimation Algorithms

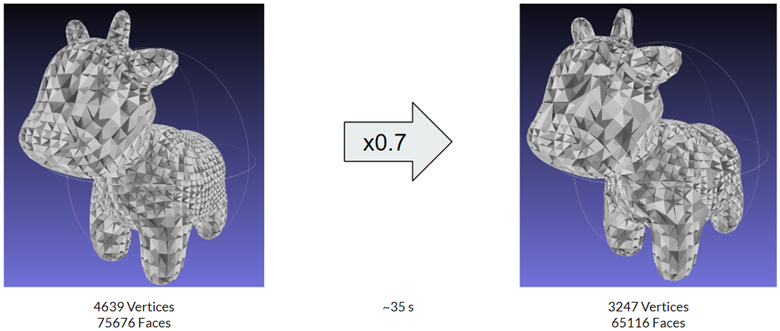
Our mesh simplification approach drew upon research in mesh and volume decimation methodologies, incorporating both the Garland-Heckbert method for mesh decimation using quadric error metrics and the Van Gelder method for volume decimation of tetrahedral meshes. We implemented these algorithms in our project, with either the Garland-Heckbert method applied to the triangular mesh of the input STL file or the Van Gelder method to the tetrahedral mesh following tetrahedralization. After evaluating and comparing their performance, we ultimately chose the Van Gelder volume decimation method, as it better suited the nature of our simulation and delivered superior results when working with volume-based algorithms.

Physics Simulation using Finite Element Method (FEM)

To perform physics simulations on the decimated mesh, we used a finite element method (FEM) non-linear physics simulation. This algorithm accepts a decimated tetrahedral mesh, applies an elastic material, and uses specified boundary conditions and external forces to solve for new vertex locations of the non-static elements in the input mesh, simulating how the mesh would deform under the specified conditions.

Weighted Handles and the K-D Tree Structure

To mirror the simulation deformation from the decimated mesh to the target mesh, we employed weighted handles inspired by their ability to quickly deform meshes, as well as the KD Tree data structure for acceleration. Handles were sampled from the surface of the decimated mesh before running FEM, and the KD Tree structure helped approximate similar locations to place the handles on the target mesh. After running FEM on the decimated mesh, we applied the deformation to the corresponding handles on the target mesh, effectively mirroring the FEM deformation.

Experiment

We experimented with different settings for decimation amount and handle sampling methods to achieve visually accurate results. The mesh decimation algorithms performed well, and we found that placing handles on the surface of our meshes was most effective. In testing, we discovered that under large forces, our simulation became increasingly inaccurate. However, we found that scaling the force applied to the decimated mesh based on the decimation amount would improve accuracy.

Conclusion

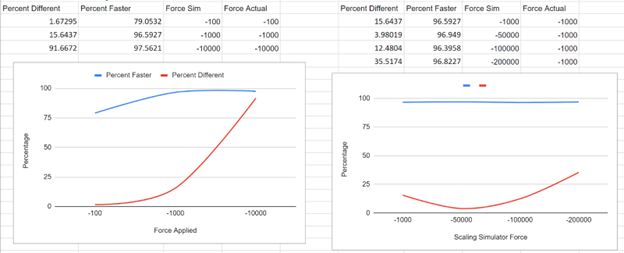
Our algorithm effectively reduces the computational cost of FEM simulation, thus reducing the required time to run such simulations. We achieved visually accurate approximations, cutting time from iterative workflows that employ the use of FEM. For future work, we could explore an implementation of Van Gelder that includes a surface geometry metric or analyze our system with dynamic FEM.

Sources

Allen Van Gelder et al., “Volume Decimation of Irregular Tetrahedral Grids.” https://users.soe.ucsc.edu/~avg/Papers/decimation-cgi99.pdf.

Michael Garland et al., “Surface Simplification Using Quadric Error Metrics.” SIGGRAPH ‘97, 1997, https://www.cs.cmu.edu/~./garland/Papers/quadrics.pdf.